How to Improve Math Performance for All Learners – Master Number Concept and Numbersense

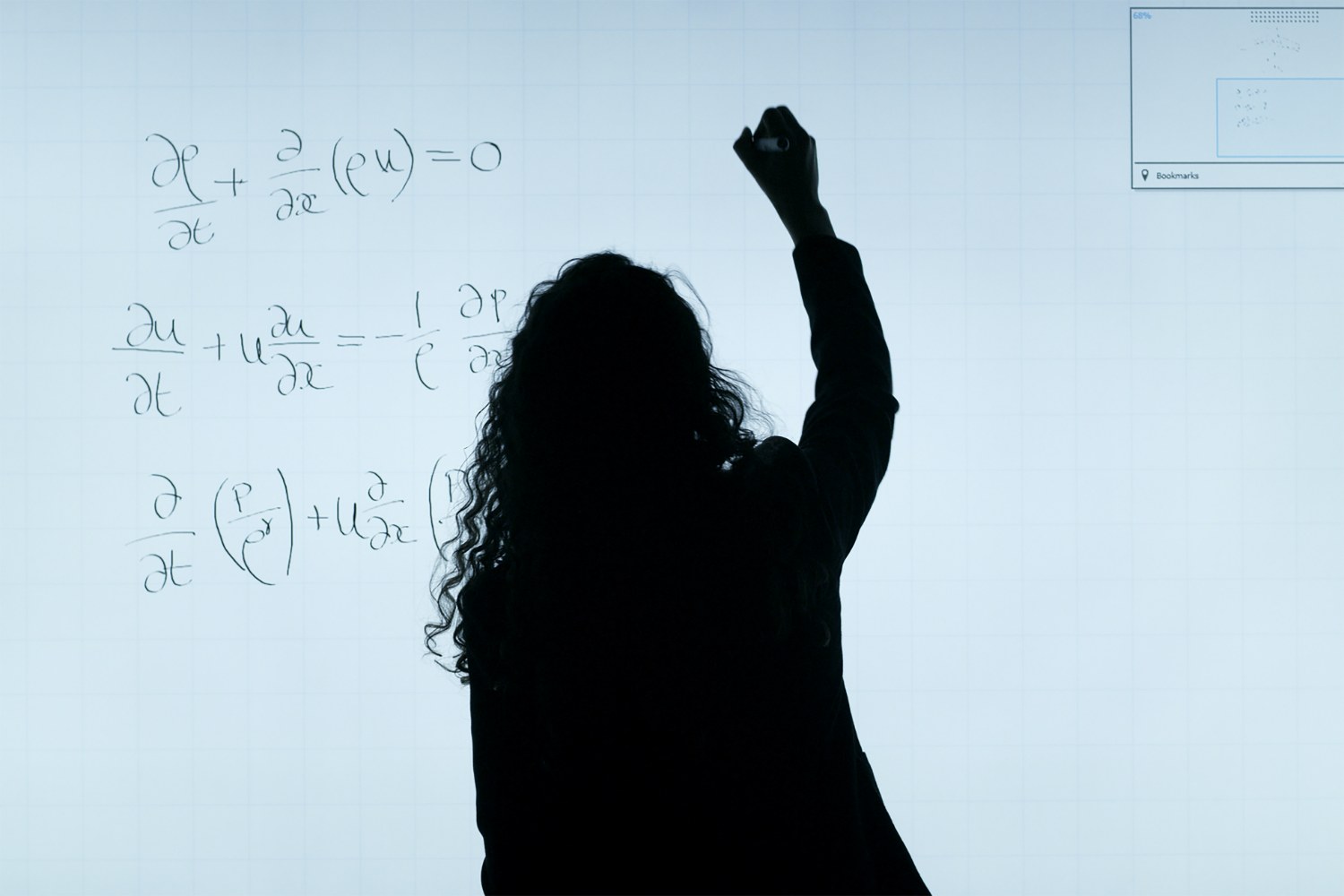
With true numberness with decomposition and recomposition as the basis, one can easily learn the arithmetic facts, particularly, addition/subtraction facts. The concept of visual cluster and the decomposition/ recomposition is the phonological equivalent of numbersense.

Weaker a child’s decomposition/ recomposition skill and automatic fact recognition skills, the more the child has to rely on inefficient strategies such as counting. And the compensatory use of inefficient strategies will never entirely make up for weak decoding, and even the most adapt compensator remains at an enormous disadvantage.

Similarly, rote practice of arithmetic facts and procedures is not productive. Practicing a skill over and over in the same way may teach students to acquire the skill. But it won’t necessarily lead them to apply that skill to other contexts. Rather, students need to practice the skill in a variety of different ways using efficient strategies to be able to retain, generalize and apply that information.

Social and Academic Expectations about Numeracy

To be fluent in numeracy, one of the components is having good numbersense. One’s open, positive, and flexible attitude toward number and the ability to display that flexibility and proficiency in handling quantity is called numbersense. As a skill set, numbersense refers to a person’s ability to look at the world quantitatively and make quantitative and spatial judgements and decisions using mental calculations using the properties of number.

Numbersense consists of a cluster of ideas such as the meaning and ways of representing numbers, relationships among numbers, the relative magnitude of numbers, and proficiency in working with them (ultimately leading to mastering arithmetic facts and their usage). Numbersense is not a set of discrete skills but a set of integrative skills.

Strategies and instruction in arithmetic facts and procedures are much more productive when a child has acquired the number concept properly.

Students with good numbersense can move effortlessly between the real world of numbers and formal numerical expressions. They can represent the same number in multiple ways depending on the context and purpose. In operations with numbers, children with a good sense of number can decompose and recompose numbers with ease and fluency. Technically, it is the integration of (a) number concept, (b) number relationships (arithmetic facts), and (c) place value. Its mastery should reflect age and grade specific expectations, needs, and facility with number. It gets more and more complex and sophisticated as a person encounters new number systems.

For example, at the end of Kindergarten the expected mastery of numbersense is (a) number concept, (b) 45 sight facts, and (c)place value of 2-digits. Similarly, mastery of numbersense expected by the end of first grade is: (a) number concept, (b) 100 Addition facts (sums up to 20), and, (c) Place value of 3-digits. And, numbersense, at the end of fourth grade is (a) number concept, (b) All arithmetic facts (addition, subtraction, multiplication, and division), and, (c) Place value up to the hundredth place.

Counting is like recognizing and decoding individual letters and their sounds, and recognizing visual clusters for individual numbers is like recognizing phonemes and even words.

Through organized practice and experiences in various forms such as algorithms/ procedures, this proficiency and fluency in numbersense is translated into numeracy. Numeracy is a child’s ability and facility in arithmetic operations (addition, subtraction, multiplication and division) on whole numbers correctly, consistently, fluently, in multiple forms of procedures, including the standard algorithm with understanding. By the end of fourth grade, a child should have mastered numeracy.

If a student has deficits in it at the end of fourth grade, he needs intervention. That intervention should focus on developing, number concept, arithmetic facts, place value and then numeracy with the proper language, conceptual schemas, strategies based on decomposition/recomposition and place value, multiples procedures appropriate to the context of the problem.

Dyscalculia and Acquired Dyscalculia

There are several reasons for the incidence of specific mathematics learning difficulties from language related to neuropsychological and cognitive reasons to environmental reasons. However, understanding the development of numbersense provides a window into children’s arithmetic difficulties, particularly dyscalculia. Most of the difficulties in mathematics, particularly, arithmetic emanate from the difficulties in learning of number related difficulties.

Dyscalculia is a child’s difficulty in conceptualizing and using number, mastering number relationships, and producing outcomes of number operations. The difficulty with numbersense may be the result of a child’s assets (or lack thereof)— neurological, neuropsychological, and cognitive reasons, and/or environmental factors—poor teaching, poor curriculum, or lower expectations. When these difficulties exist in spite of a child having intact neurological, neuropsychological, or other cognitive factors, then it is purely because of environmental factors and this will be termed as acquired dyscalculia.

Dyscalculia or acquired dyscalculia, thus are the manifestation of difficulties in the integration of number concept, numbersense, and numeracy. However, just like effective teaching methods for reading can mitigate the impact of dyslexia, similarly, one can have dyscalculia or acquired dyscalculia. But effective and efficient teaching methods can give students skills so that the effects of dyscalculia and acquired dyscalculia (and other specific mathematics difficulties) are minimized or mitigated.

Dyscalculia is a quantity/number (with some overlap of spatial orientation/ space organization) based disorder, so the intervention and remedial programs should focus on the development of number concept, numbersense, and numeracy. That means, the interventions and remedial instruction for children with learning disabilities (including dyscalculics) initially should focus on the mastery of number concept—visual clustering, decomposition/recomposition, and acquiring the sight facts.

To design effective methods, understanding the definitions and characteristics of dyscalculia is critical. For example, children, especially gifted children, may be able to compensate for even massive deficits using one or more of their equally massive strengths.

A child with tremendous memory and fantastic oral comprehension might be able to get around abysmal arithmetic fact fluency for a while to produce an adequate arithmetic result when mathematics is still fairly simple.

But if they have deficits in the understanding, fluency and applicability of number concept and numbersense and procedures, they will have difficulty in future mathematics. Similarly, a child with using counting methods may be able to do well on tests and exams, in the early grades. But she will have difficulties later on.

Unfortunately, many school personnel often get this wrong as their own understanding of dyscalculia and arithmetic disability may be limited affecting resources available for such in quantity and quality. This is compounded by the inadequate preparation of special education teachers in mathematics and mathematics learning disabilities, particularly dyscalculia compounding the environmental factors related to dyscalculia.

Many parents and school personnel mistakenly assume that dyscalculia equates to permanent condition of deficit or disability. True number concept is at the basis of the development of fluent numbersense. Therefore, the condition of dyscalculia and acquired dyscalculia can be compounded without proper teaching of number concept.

It is very difficult to master (understanding, fluency and the ability to apply), arithmetic facts and procedures without proper number concept teaching.

Catch Them Before They Fall

Early identification and assessment of number concept and numbersense are essential to prevent numeracy failure in young children and avoiding future mathematics difficulties. Students without adequate mastery of sight facts and decomposition/recomposition early, continue to demonstrate poor numbersense and numeracy skills, even into the middle grades and high school.

There is a strong predictive validity to early number concept (particularly decomposition/ recomposition) and later mathematics achievement. The contribution of sight facts and decomposition/recomposition role does not diminish. Children continue to use the number concept and decomposition/ recomposition whenever they encounter numeracy problems. For example, when students encounter work on fractions, integers and rational numbers, they continue to need and use them for new number relationships.

The key element is the constant and intense practice in phonemic awareness that helps students to connect graphemes and phonemes.

Research in reading processes indicates that certain domain-specific deficits such as measures of a child’s phonemic awareness and phonological sensitivity are the best predictors of early reading performance (better than IQ tests, readiness scores, or socioeconomic level). It is widely accepted that deficits in phonological processing are the proximal cause of Reading Disability (RD) (Vellutino, Fletcher, Snowling, & Scanlon, 2004)).

Similarly, a domain-specific deficit in processing numerosities (numberness) has been implicated in mathematics disabilities (MD), such as dyscalculia (Butterworth, 2010; Wilson & Dehaene, 2007). And of the several sub-skills of numberness the most important skill involved as a deficit is decomposition/ recomposition.

In addition, domain-general cognitive risk factors, such as slow processing speed and working memory might be shared between the two disorders and could possibly explain why they may co-occur. Research shows that almost 40% of dyslexics also exhibit symptoms of dyscalculia.

This comorbidity between RD and MD indicates that there is fundamental components in both of them that implicate. These are phonemic awareness and decomposition/recomposition, respectively. We have observed, with hundreds of children, that fluent numberness (integration of oneto-one correspondence with sequencing, visual clustering, and decomposition/ recomposition) is a better predictor of future proficiency and fluency in arithmetic and even higher mathematics. Remediation of numberness related key skills results in better understanding and mastery of numeracy.

Early identification and assessment of number concept and numbersense are essential to prevent numeracy failure in young children and avoiding future mathematics difficulties.

On the other hand, high comorbidity rates between reading disorder (RD) and mathematics disorder (MD) indicate that, although the cognitive core deficits underlying these disorders are distinct, additional domain-general risk factors might be shared between the disorders.

Three domain-general cognitive abilities processing speed, temporal processing, and working memory are studied in RD and MD. Since attention problems frequently cooccur with learning disorders, the three factors associated with attention problems account for the comorbidity between these disorders. However, the attention problems observed in the case of MD, some of them are secondary in the same sense, that they might be the byproduct of consistent failure in mathematics.

Research on measures of processing speed, temporal processing, and memory with primary school children with RD, children with MD, children with both disorders (RD+MD), and typically developing children (TD controls) show that all three risk factors are associated with poor attention.

After controlling for attention, associations with RD and MD differed. Although deficits in verbal memory were associated with both RD and MD, reduced processing speed was related to RD, but not MD. The association with RD was restricted to processing speed for familiar nameable symbols.

In contrast, impairments in temporal processing and visuospatial memory were associated with MD, but not RD. Visuospatial memory is essential for visual clustering, decomposition/recomposition, and therefore with development of sight facts.

Interventions and Remedial Strategies for Dyscalculia

To help LD students, particularly poor readers, become fluent readers, few key components are typically involved. These include: (a) constantly increasing sight vocabulary; (b) sustained, systematic work on phonics and phonological sensitivity as a means to ‘breaking the code’ and build proficiency by focusing on phonemic awareness; and (c) repeated readings using efficient strategies for blending sounds to build fluency.

The key element is the constant and intense practice in phonemic awareness that helps students to connect graphemes and phonemes. This process helps children to move from decoding of individual letters to chunking and blending sounds. This insight helps interrupt the cycle of failure for poor readers.

Dyscalculia is a child’s difficulty in conceptualizing and using number, mastering number relationships, and producing outcomes of number operations.

Many planners of mathematics instruction for young children often do not fully take into account that to increase proficiency, competence, and fluency with basic addition and subtraction facts, children need to develop solid number concept (numberness) and flexible numbersense. They stop short: as soon as children are able to count one-toone, they assume the child has the concept of number. Sequential counting and one-to-one correspondence, even when it is converted into conservation of number is not enough for competence in numbersense.

For example, explicit teaching of phonemic awareness skills and sound blending skills is important, but instruction that integrates ‘in how to blend phonemes together’ and also how to ‘pull apart’ or ‘segment words into phonemes’ is more useful to students in order to acquire reading skills. The organized and intense supervised practice in building sight vocabulary, “pulling apart” and “blend it together” converts novices into fluent readers.

Similarly, learning sequential counting, oneto-one correspondence, visual clustering, building sight facts, and decomposition/ recomposition in isolation are useful to an extent, but what is even more important and productive is instruction that focuses on their integration. An organized and early intensive supervised practice in the integration of these component skills develops true number concept (numberness) and then aids in the optimal development of numbersense.

When one hears or sees a number, one does not see discrete objects; instead, one sees or hears a collection represented in its abstract symbolic form. Children can count objects one-by-one, but they have difficulty recognizing visual clusters of objects as represented by specific numbers. Counting is like recognizing and decoding individual letters and their sounds, and recognizing visual clusters for individual numbers is like recognizing phonemes and even words.

Decoding individual letters does not make a child a fluent reader. For proficiency and fluency in reading with comprehension, one needs grapheme-phoneme connection and practice in blending sounds. Similarly, counting does not make a child fluent in numberness or numbersense. One has to blend numberness of two numbers (sight and addition facts) to produce new numbers. Arithmetic facts (blending of two numbers) and place value (blending of two or more numbers) are like identifying the phonemes in a big word and then blending of those sounds in reading that word.

Weaknesses in phoneme awareness, rapid automatized naming and working memory are strong and persistent correlates of literacy problems, particularly spelling, even in adults. Similarly, decomposition/ recomposition, working memory, and rapid automatized naming are related to addition and subtraction facts and then with multiplication and division facts.

Strategies and instruction in arithmetic facts and procedures are much more productive when a child has acquired the number concept properly. Further, true number concept and decomposition/recomposition is the basis of deriving addition and subtraction strategies [Making ten, N + 9 (add 10 – 1), N+N (doubles), N + (N+1) (doubles plus 1), N + (N – 1) (doubles minus 1), N + 2 ( 2 more), (N + 1) + (N – 1) (2 apart)]. Mastery of arithmetic facts, thus, is dependent on number concept, decomposition/recomposition, and strategies based on these.

For example, 8 + 6 = 8 + 2 + 4 (applying the knowledge that we need 2 to make 10 and 6 is decomposed into 2 + 4) = 10 + 4 (8 and 2 are recomposed into 10 and with the knowledge of teen’s numbers —place value to get 14), or 8 + 6 = (7 + 1) + 6 = 7 + 7 = 14, or 8 + 6 = 2 + 6 + 6 = 2 + 12 = 14, or 8 + 6 = 8 + 8 -2 = 16 – 2= 14. All of these strategies are built on sight facts, making ten, and decomposition/ recomposition.

As phonemic awareness is to reading, decomposition/recomposition is to numbersense and numeracy. The reading research demonstrates phonemic awareness (PA) is one of the biggest building block of the reading success, and decomposition/ recomposition process is the building block to mathematics. And, PA should not be abandoned until the child has demonstrated advanced levels of PA skills. However, decomposition/ recomposition, as a process, is present in mathematics at all levels. It is never abandoned.

A skilled reader is able to read almost every word without activating the phonological processor. Fluent reader reaches that point because she did use the phonological processor which allowed her to make words automatic. There is a real difference between a beginning reader and a fluent reader. Looking at a cluster of objects (up to ten) and recognizing it and giving it a numerical name, instantly, is the goal, but to get there we need to focus on recognizing smaller clusters and even some counting.

As in reading a word, we do not focus on each letter, nor we begin with the whole word memorization, similarly, in numberness, we neither focus on one object at a time nor on the whole cluster to start with.

Number sense is not a set of discrete skills but a set of integrative skills. Students with good number sense can move effortlessly between the real world of numbers and formal numerical expressions.

Thus, the acquisition of number concept and then acquiring arithmetic facts, at one level, is similar to learning to read. One acquires the meaning of symbols, decodes the symbols and then combines the symbols to relate to other symbols. In reading, it is the process of associating phonemes to grapheme and viceversa and the blending of sounds.

When a child encounters a new word, she breaks the word into ‘chunks’ and then ‘blends’ these chunks into the word. This chunking and blending is the manifestation of the integration of grapheme-phoneme relationship. A child cannot become a fluent reader without being fluent in graphemephoneme association and the process of ‘chunking’ and ‘blending’.

The parallel process in mathematics is also three-fold: (a) instantly associating a visual cluster with its number representation, (b) associating a sound with number, and (c) decomposition and recomposition. The recognition of a visual cluster and decomposing a cluster into its subclusters and combining sub-clusters into a larger cluster and instantly recognizing the larger cluster as the combination of the subclusters are the key processes to acquiring the number concept and numbersense.

In most situations, in teaching number, teachers help children acquire the concept of number by connecting the phoneme (sound s-e-v-e-n) with grapheme (symbol 7). But that is not enough because acquiring numberness is more than learning to read a number or even count. This causes the manifestation of the symptoms of dyscalculia and acquired dyscalculia in most children.

Thus, the acquisition of number concept and then acquiring arithmetic facts, at one level, is similar to learning to read.

In teaching letters, there are two schools/ traditions. In England, the sound of letters are taught first and then the letters, in most American schools, the letters first and then their sounds. In reading research, there is higher correlation between sound/letter to reading than letter/sound relationship. There is great deal of evidence that both are important.

Similarly, in the United States, the number names are taught first and then the numerosity associated with them. In contrast, in Asia and England, it is the numerosity first and then the number shapes. Both are essential for learning number concept. However, when numerosity and oral representation are learnt before the writing of numbers, children develop number concept faster. The judicious integration of the two expedites the process.